В.Г. Градецкий, д-р. техн. наук, Л.Н. Кравчук,
гл. спец.-констр.,
М.М. Пушкин, канд. техн. наук,
Институт проблем
механики РАН, Москва
ДИНАМИЧЕСКИЕ ПРОЦЕССЫ В МНОГОЗВЕННЫХ МИКРОСИСТЕМАХ
|
Представлены результаты исследований динамических процессов в многозвенных микросистемах. Рассмотрены и оценены силы, обуславливающие движение и силы сопротивления движению в различных средах для микросистем. Представлена математическая модель микроробота-капсулы при ее движении за счет перистальтики, учитывающая запаздывание. Математическая модель является системой нелинейных дифференциальных уравнений с запаздывающим аргументом, содержании как обыкновенные дифференциальные уравнения, так и уравнение в частных производных Решение этой системы возможно на основе численного моделирования. Исследовательская работа выполнялась при поддержке Российского фонда фундаментальных исследований, проект РФФИ 99-01-00085. |
Упрощенные схемы многозвенных микросистем-микророботов
Анализ сил, действующих на микросхваты
Движение микросистем в различных средах
Введение
Несмотря
на опубликованные в последнее время некоторые результаты исследования движения
микросистем [1-4], динамические процессы с учетом особенностей влияния окружающей
микросреды исследованы недостаточно. Очевидно, что движение микросистем, в том
числе микророботов, определяется прежде всего их механической структурой и характеристиками
среды
[5-7]. В качестве объектов для исследования выберем достаточно распространенные
механические системы, а именно, многозвенные микросистемы, представляющие собой
управляемые гибкие стержни, соединенные шарнирами со встроенными в них микродвигателями,
и, прежде всего, рассмотрим некоторую их упрощенную модель – двухзвенный робот
с упругими связями. Ранее была выявлена характерная особенность движения подобного
типа роботов, состоящая в необходимости учета последствий или запаздывающих эффектов
в динамике исследуемой модели, что привело к целесообразности описания движения
двухзвенного робота системой уравнений с запаздывающим аргументом [6]. Затрудняющим
исследование динамики двухзвенного робота фактором являлось то, что реальное движение
системы происходит в среде с неизученными или неизвестными априори свойствами,
точное знание которых на этапе проектирования микросистем затруднено.
В связи с этим обстоятельством необходимо более детальное изучение среды, в которой происходит движение и введение в синтезируемый закон управления движением робота принципов адаптации или нечеткой логики [2,6-9].
Принимается во внимание, что синтезируемые законы управления движением миниатюрных роботов на основе теории адаптации могут быть распространены на другие миниатюрные механические системы, функционирующие в условиях недетерминированного воздействия окружающей среды.
Что касается технического применения микро- и мини-роботов, то здесь необходимы исследования динамических процессов, возникающих при движении миниатюрных роботов внутри труб малого диаметра как с жесткими, так и деформируемыми стенками, обладающими упругой податливостью. Движение таких роботов, как правило, осуществляется собственными исполнительными механизмами.
При применении микро-роботов для целей медицинской диагностики необходимость использования собственных движителей робота отпадает, поскольку используется энергия, например, перистальтического сокращения желудочно-кишечного тракта (ЖКТ), в результате чего происходит проталкивание микро-робота по ЖКТ, или энергия потока крови внутри кровеносных сосудов, что приводит к общему, вместе с кровью, движению мини-робота.
Как первый аспект, технический, так и второй аспект, медицинский, применения микророботов характеризуется тем, что для построения законов управления такими микророботами необходимо учитывать, что их движение происходит в средах с априори неопределенными параметрами и при наличии существенных эффектов запаздываний.
Отражением этого в математических моделях движения микророботов будет тот факт, что уравнения, а это, как правило, дифференциальные уравнения или системы дифференциальных уравнений, будут содержать в своих коэффициентах априори неопределенные добавки, связанные с неопределенностью среды, а сами уравнения будут уравнениями с запаздывающим аргументом, что связано с теми или иными инерциальными эффектами.
Эти два момента являются, конечно, осложняющими при построении математических моделей движения микророботов. Но отсутствие собственных движителей медицинских микророботов несколько упрощает, относительно технических микророботов, исследование и создание таких систем.
Для рассмотрения вводятся упрощенные схемы микросистем, для которых исследуются проблемы динамики.
В данной работе, исходя из перечисленных выше практических задач применения микро- и мини-роботов, рассматриваются такие аспекты динамики, как анализ сил, действующих на микроробот через микроопору или микрозахват, движение моделей микророботов в жидкой среде и приближенная математическая модель движения микроробота-капсулы под действием перистальтики желудочно-кишечного тракта.
Упрощенные схемы многозвенных микросистем-микророботов
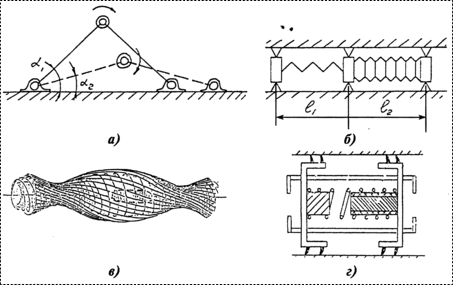
Выбранные для исследования динамики принципиальные схемы микросистем — мини- и микророботов (рис. 1) содержат два или большее число звеньев, которые соединены между собой шарнирами или механическими системами с вмонтированными приводными двигателями в узлах-шарнирах, либо приводящимися в движение за счет колебаний пьезоэлектриков, или сокращения упругих стенок оболочек, либо перемещающихся в результате подачи давления сжатого воздуха.
|
|
| Рис.
1. Упрощенные схемы микророботов: |
Движение двухзвенного микроробота по жесткой поверхности (рис. 1,а) осуществляется за счет поочередного освобождения стоп и вращения микродвигателя в шарнирах. В другой модификации (рис. 1,б) движение осуществляется за счет подачи сжатого воздуха в сильфон первого из закрепленных с помощью схватов звеньев и последующего движения второго звена за счет пружины.
В других случаях движение осуществляется за счет последующих сжатий и ослаблений стенок эластичной оболочки (рис. 1,в), как это происходит при движении автономной микрокапсулы внутри желудочно-кишечного тракта относительно продольных и круговых гладкомышечных волокон.
Движение микроробота внутри трубы с жесткими стенками (рис. 1,г) осуществляется за счет генерации колебаний в конечных звеньях, выполненных из пьезоэлектрических пластин, соприкасающихся со стенками.
Анализ сил, действующих на микросхваты
При рассмотрении влияния различных сил, вынуждающих двигаться микросистемы или тормозящих их движение в различных условиях окружающей среды, рассмотрим прежде всего такие, которые могут существенно влиять на процесс движения.
К таким силам можно отнести силы взаимодействия стоп или схватов микророботов с шероховатыми поверхностями, силы поверхностного натяжения жидкостей, электростатические силы и силы электростатического притяжения, силы трения и адгезии, силы упругости, а также дополнительные движущие силы, определяемые приводными устройствами микросистем, и силы сопротивления, зависящие от параметров внешней среды и от конструктивных характеристик.
Движение микросистем в различных средах
Движение по твердой поверхности. В общем случае движение микросистем по твердой поверхности как движение твердого тела описывается уравнением Лагранжа второго рода [10]
,
,
где
–
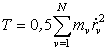кинетическая энергия системы 
материальных точек.
Величины 
, 
(
) –
это обобщенные координаты и обобщенные скорости рассматриваемой микросистемы.
Скорости точек 
выражаются через обобщенные скорости,
а также через независимые координаты и время с помощью формулы
,
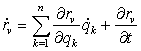где
, – число движущихся материальных точек, из которых
состоит рассматриваемая система.
В левые части уравнений
Лагранжа после выполнения операции дифференцирования по времени – входят 
время 
,
обобщенные координаты , обобщенные скорости 
, и
обобщенные ускорения 
, ().
Обобщенные
силы 
, стоящие в правых частях
уравнений Лагранжа, обычно задаются как функции , 
,
(
)
.
Уравнения
Лагранжа образуют систему из 
обыкновенных
дифференциальных уравнений второго порядка с независимыми
функциями от независимого переменного .
Порядок этой системы равен 
. Заметим, что система
дифференциальных уравнений, определяющая движение голономной системы с степенями
свободы, не может иметь порядок, меньший чем 
, так как в
силу произвольности начальных условий для и , ,
решение должно содержать произвольных постоянных.
В
случае несвободной системы подлежат определению еще реакции 
, . Реакции не входят в
уравнения Лагранжа. Это является существенным преимуществом последних. После того
как уравнения Лагранжа проинтегрированы и найдены функции ,
, определяют радиус-векторы 
системы
движущихся материальных точек, а следовательно,
определяют и , 
и 
, где
– равнодействующая всех активных сил. После этого
неизвестные реакции определяются из формул:
.
В случае свободной системы материальных точек уравнения Лагранжа представляют собой компактную форму записи уравнений движения в произвольной системе координат.
При переходе к микросистемам необходимо к рассмотренным выше силам добавить силы "микромира", которые или побуждают к движению рассматриваемую систему, или тормозят ее продвижение. К таким силам можно отнести силы трения и силы адгезии, силы поверхностного натяжения жидкостей, электростатические силы притяжения и отталкивания и ряд других сил.
Явление адгезии и адгезионные силы. Считается, что адгезия – это связь или взаимодействие между поверхностями двух разнородных контактирующих тел. Для нарушения этой связи необходимо внешнее воздействие определенного значения. Адгезия обуславливается прежде всего различными видами взаимодействия между молекулами или атомами. Эти взаимодействия приводят к образованию межмолекулярной и химической связей. Природа межмолекулярной связи, которую иногда называют ван-дер-ваальсовым взаимодействием, возникает за счет ориентационного, индукционного и дисперсного взаимодействий, которые имеют электромагнитную природу.
Химическая связь может реализоваться за счет донорно-акцепторных переходов, т.е. в результате передачи и приема электронов молекулами контактируемых поверхностей, а также за счет ионной и ковалентной связей.
Кроме межмолекулярных взаимодействий контактирующих поверхностей возможно электростатическое взаимодействие, обусловленное действием кулоновских сил. Электрические силы могут выступать в качестве связи, обуславливающей адгезию в том случае, когда контактирующие поверхности несут избыточные заряды. В этих условиях возникает электрическая компонента за счет кулоновских сил, которая и обуславливает адгезию.
Проявление различных связей зависит от свойств среды. В газовой и жидкой средах адгезия обусловлена, главным образом, межмолекулярными и донорно-акцепторными связями. Помимо адгезионной связи в жидкостной среде появляются дополнительные силы, связанные как с расклинивающим действием тонкого слоя жидкости между поверхностями, что приводит к снижению сил адгезии, так и с возникновением довольно значительных капиллярных сил как результата сил поверхностного натяжения.
Ионные и ковалентные связи наблюдаются сравнительно редко и мало оказывают влияние на адгезию. Кулоновские силы действуют в основном в газовой (воздушной) среде. В жидкости, имеющей электролиты, которые являются проводниками, влияние кулоновских сил на адгезию, вследствие утечки зарядов, ничтожно мало.
|
|
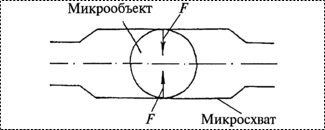
| Рис. 2. Взаимодействие между сферическим заряженным объектом и поверхностью схвата |
Рассмотрим взаимодействие между сферическим заряженным объектом и поверхностью схвата (рис. 2).
Сила между сферическим заряженным объектом (диэлектриком) и поверхностью схвата
,
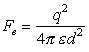где
– заряд;
–
диэлектрическая проницаемость, 
см-2,
–
диаметр сферы. Если материалом схвата является кремниевое соединение или слюда,
то диэлектрическая проницаемость 
см-2
при давлении 
Па и зазоре 
мкм.
Силы адгезии, возникающие при соприкосновении шара и плоскости [11], могут быть рассчитаны по формуле
,
где
– константа
Лифшица – Ван-дер-Ваальса; 
– микрозазор между поверхностями; – диаметр сферы. Во влажной среде между сферическим
объектом и плоскостью возникают довольно значительные
капиллярные силы как результат поверхностного натяжения
,
где
мН×м-1 – коэффициент поверхностного
натяжения для воды; – зазор между поверхностями;
, и 
– углы контакта
между жидкостью и поверхностями.
Если предположить, что зазор значительно меньше, чем радиус объекта, то
,
где
– радиус объекта.
Если сфера выполнена из кремния, то можно оценить гравитационные силы, равные
,
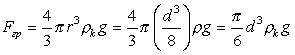где
кг×м-3 – плотность кремния.
|
|
|
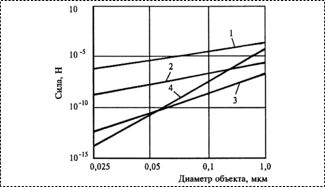
Рис. 3. Сравнение действия сил между сферой диаметра
d и поверхностью схвата: |
Сравнивая действующие силы
(рис. 3), было установлено, что для гладких поверхностей без учета шероховатости,
силы адгезии на порядок меньше, чем гравитационные силы. Капиллярные силы доминируют
и их следует уменьшать за счет конфигурации стенок захвата. Однако для гладких
поверхностей силы адгезии начинают значительно влиять при зазорах, соответствующих
диаметру объекта 50 мкм. В этом случае можно избежать генерируемого электростатического
заряда, возникающего в результате контакта для объектов манипулирования с 
мкм.
Из рассмотрения рис. 3 следует, что гравитационные и электростатические силы возрастают
значительно при увеличении диаметров объектов от 5 мкм до 1 мм. Силы адгезии оказывают
существенное влияние по сравнению с другими силами при уменьшении размеров деталей
до менее 0,05 мкм. Для уменьшения силы поверхностного натяжения можно работать
в вакууме или существенно уменьшить влияние влажности. Электростатические силы
влияют при увеличении радиуса объекта на порядок. Шероховатость
значительно важнее принимать во внимание при учете сил Ван-дер-Ваальса, чем при
учете электростатических сил.
Движение
шара в жидкости. Рассматривается
случай, когда число Рейнольдса существенно меньше единицы, т.е. 
.
Это характерно для движения микророботов в
большинстве сред. Поэтому в уравнении Навье-Стокса можно пренебречь членом 
.
Силами инерции и гравитации при движении микроробота можно пренебречь.
Тогда движение будет полностью описываться системой уравнений
,
,
где
– оператор
Лапласа; 
– вязкость жидкости; 
– относительная скорость; 
–
давление.
Вводя сферическую систему координат, из решения
написанной выше системы уравнений можно получить выражение для давления и
для действующей на шар силы 
.
;
.
Для
плавающего робота при обтекании его ламинарным потоком затрачиваемая мощность
равна 
.
Если
предположить, что скорость и размеры пропорциональны характерной длине 
, то 
и при 
мм
имеет порядок 10-8 Вт, что представляет собой весьма малую величину.
Для сравнения, подъемная сила в воздухе, которая должна быть не менее силы сопротивления для крыла летающего микроробота в воздухе, определяется формулой Жуковского
,
где
– коэффициент
сопротивления; 
– плотность воздуха; –
относительная скорость; 
– площадь крыла. Подъемная сила должна
уравновесить вес робота. В этом случае скорость и мощность пропорциональны 
.
Устройство автономного микроробота-капсулы для исследования ЖКТ. Устройство для исследования ЖКТ относится к медицинской диагностической технике и предназначено для определения рН среды, давления, температуры и скорости прохождения пищи по желудочно-кишечному тракту с одновременной пространственно-временной регистрацией того или иного химического или физического параметров в ЖКТ. Кроме того, автономная капсула может быть использована в качестве транспортного средства доставки лекарства в нужную точку ЖКТ.
Микроробот-капсула представляет собой исследовательский комплекс эндорадиозондирования, состоящий: из автономной мини-радиокапсулы с датчиками измерения необходимых химических и физических величин с пространственно-временной привязкой; электронных блоков, преобразующих и передающих полученную информацию, съемного медицинского пояса пеленгатора, который на период исследования закрепляется на животе пациента; приемно-анализирующей аппаратуры.
Предлагаемое устройство может применяться как в стационарных условиях (специальные врачебные кабинеты), где расстояние от пациента до приемно-передающей аппаратуры не превышает 3 м, так и в условиях перемещающегося пациента, где эти расстояния уже могут быть 250-500 м с использованием дополнительного усилителя передаваемых сигналов.
Более подробно об устройстве автономного микроробота-капсулы и о возможности его создания можно узнать из работы [6].
Математическая модель движения микроробота-капсулы под действием перистальтики ЖКТ
В настоящем разделе статьи предпринята попытка построения математической модели движения микроробота-капсулы (в дальнейшем просто капсулы) по ЖКТ. Мы оставляем в стороне вопросы, связанные с динамикой капсулы в условиях априори неопределенной среды в ЖКТ. Основное внимание будет уделено вопросам движения капсулы под действием перистальтики ЖКТ.
Опишем кратко механизм перистальтических сокращений ЖКТ. Было обнаружено, что ответ кишечника на локальное раздражение состоит из сокращений, возникающих выше места раздражения, и расслабления, наблюдающегося ниже стимулируемой области. Этот феномен в медицине известен как "закон кишечника". В соответствии с ним перистальтика кишечника состоит в последовательных сокращениях стенки кишки в ответ на локальное раздражение. В ЖКТ перистальтические сокращения наслаиваются на другие виды мышечной активности, в частности на ритмичные сегментообразные сокращения. Ритм и скорость распространения перистальтических волн в различных отделах ЖКТ неодинаков. Перемещение в ЖКТ автономной радиокапсулы происходит благодаря ритмическим сокращениям системы мышц стенок пищевода, желудка, кишечника, что обеспечивает перемещение радиокапсулы вместе с их содержимым в каудальном направлении. В общем случае, благодаря наличию спирально расположенных продольных мышц и круговых (циркулярных) мышц, радиокапсула осуществляет вращательно-поступательное движение, т.е. движение капсулы происходит по спирали.
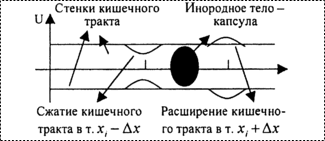
Мы рассмотрим один из видов перистальтического сокращения стенок тонкого кишечника, при котором перенос пищевого субстрата осуществляется за счет так называемых пропульсивных перистальтических движений, представляющих собой сокращения циркулярных мышечных слоев. Эти движения распространяются вдоль пищеварительного тракта наподобие волны. Обычно такой волне сокращения предшествует волна расслабления. Это схематично показано на рис. 4.
|
|
| Рис. 4. Одномерная динамика ЖКТ |
Ось OX – направление вдоль кишечного тракта; ось OU – направление сжатия-расширения кишечного тракта.
Рассмотренный выше механизм перистальтики позволяет нам предположить, что волна сокращений кишечного тракта подобна волне упругих колебаний струны, которая в рассматриваемой нами системе координат описывается известным уравнением гиперболического типа
,
где
– функция,
описывающая значение отклонения стенки кишечника от положения равновесия в точке
с координатой 
в момент времени ; 
–
скорость распространения волны сжатия кишечника, в общем случае величина переменная,
т.е. 
; 
– плотность распределения внешних сил, отнесенных
к единице массы.
Будем считать, что движение капсулы в ЖКТ происходит в жидкостной среде. Тогда уравнение ее движения будет иметь вид
,
где
– значение
смещения капсулы в момент времени ; 
–
результирующая сила сжатия, действующая со стороны кишечного тракта на капсулу
и определяющая силу проталкивания капсулы; 
– сила трения скольжения капсулы внутри ЖКТ;
–
относительная скорость движения капсулы, в общем случае величина переменная; 
–
коэффициент сопротивления движению капсулы в вязкой среде ЖКТ.
Свяжем
результирующую силу с величиной
сжатия ЖКТ линейным соотношением
,
где
– коэффициент пропорциональности.
В
силу того, что есть возрастающая
функция времени , ясно, что движение капсулы начнется не
сразу, а спустя некоторый интервал времени 
. Таким образом,
член, описывающий сопротивление среды, должен содержать запаздывание .
Тогда, согласно изложенному выше, имеем следующую систему уравнений, которая описывает движение капсулы:
,
.
Мы предполагаем наличие двух случаев:
· скорость
перемещения волны перистальтики равна скорости движения капсулы, т.е. 
;
· скорость
перемещения волны перистальтики больше скорости перемещения капсулы, т.е. 
.
В последнем случае будем считать, что волна сокращения уходит в бесконечность. Вслед за ней идет вторая волна сжатия, потом третья и т.д. Каждая из последующих волн сокращения осуществляет проталкивание капсулы Очевидно, что в первом случае скорость перемещения капсулы на "гребне" первой волны больше, чем скорость перемещения капсулы во втором случае.
Распишем полученную систему как систему трех уравнений:
· для первого случая
;
;
;
· для второго случая
;
;
.
Для этих систем необходимо задать начальные и краевые условия.
Первая система уравнений является системой нелинейных дифференциальных уравнений с запаздывающим аргументом, содержащей как обыкновенные дифференциальные уравнения, так и уравнение в частных производных.
Исследование свойств систем типа рассмотренных, особенно в условиях априорной неопределенности коэффициентов модели, является сложной математической задачей, и ее решение возможно на основе численного моделирования.
Список литературы
1. R.S. Fearing. Powering
3 Dimensional Microrobots Power Density Limitations Proceed. 1998 Tutorial on
Micro Mechatronics and Micro Robotics Workshop WS5, 1998 IEEE International Conference
on Robotics and Automation,
2. G. Muscato. Fuzzy Control of an Uderactuated
Robot with Fuzzy Microcontroller. Microprocessors and Microsystems, 23 (1999)
385-391, Elsevier, 1999.
3. Y. Utsumi. Micromachine for Medical
Application. Proc of 2-nd International Workshop on Robotics and Systems, Oct.
1998,
4. Т. Fukuda, К. Tanie, Т. Mitsuoka. A New Method of Master-Slave Type
of Teleoperation for Micro-Manipulator System / IEEE Proc. on Micro Robots and
Teleoptrators Workshop, Hyannis, Massachusetts, USA, 1987.
5. V. Gradetsky.
Survey on Medical Robotics Activity in
6. Градецкий В.Г., Кравчук Л.Н., Пушкин М.М. Движение миниатюрных роботов в условиях априорной неопределенности при наличии эффектов запаздывания. М.: ИПМ РАН. Препринт № 649, 1999. С. 1-33.
7. V. Gradetsky, М. Pushin, М. Rachkov. Control motion of two-links mobile robot with
flexible connections. Proc. of 4-th ECPD International Conference on Advanced
Robotics, Intelligent Automation and Aktive Systems, August, 1998,
8. V. Gradetsky, V. Veshnikov, S. Kalinichenko,
A. Moiseenko. Distributed Control of Multilink
9. Вешников В.Б., Градецкий В.Г., Калиниченко С.В., Лопашов В.И. Системы миниатюрных роботов. М.: ИПМ РАН. Препринт № 564, 1996. С. 1-56.
10. Гантмахер Ф.Р. Лекции по аналитической механике. М.: Наука, 1966. 300 с.
11. Зимон А.Д. Адгезия пленок и покрытий М.: Химия, 1977. 274 с.