УДК 621.373.826
В.В.Старков, канд. техн. наук, В.В.Аристов, чл.-корр. РАН, д-р
физ.-мат. наук, проф.,
ИПТМ РАН, пос. Черноголовка, Московская обл.;
А.М.Желтков, С.А.Магницкий, А.В.Тарасишин,
МГУ им. М.В.Ломоносова, Международный лазерный центр

|
Разработана технология изготовления трехмерных периодических структур
из макропористого кремния, основанная на методе глубокого фотоанодного
травления с периодической модуляцией тока травления во времени. Реализована
эффективная схема расчета оптических свойств периодических структур с
фотонными запрещенными зонами, основанная на численном интегрировании
уравнений Максвелла с помощью метода конечных разностей. Исследуются свойства
локализации поля в дефектных модах фотонных кристаллов и обсуждаются
приложения кремниевых фотоннокристаллических структур в области микроскопии
высокого разрешения, волноводной оптики, локального фотовозбуждения,
нелинейной оптики
|

Введение
Методика и результаты вычислений
Технология изготовления трехмерных
периодических структур на основе макропористого кремния
Выводы
Введение
Создание трехмерных фотонных
кристаллов [1], характеризующихся наличием запрещенных зон в спектре
пропускания в оптическом диапазоне частот, остается серьезной технологической
проблемой. В настоящее время ведутся активные исследования путей решения этой
задачи с помощью электронно-лучевой [2,3] и голографической [4] литографии,
методами двухфотонной полимеризации [5] и волоконно-оптических технологий [6],
а также с использованием коллоидных кристаллов [7] и синтетического опала [8].
Как показано в работах [9,10], один из перспективных путей создания структур с
фотонными запрещенными зонами (ФЗЗ) связан с использованием макропористого
кремния.
В настоящей статье на основе
эффективной схемы расчета оптических свойств конечных периодических структур с
ФЗЗ анализируется распределение электромагнитного поля в ФЗЗ-структурах с
дефектом решетки, а также спектр дефектных мод в запрещенных зонах фотонных
кристаллов (ФК) на основе кремния. Обсуждаются приложения кремниевых
фотоннокристаллических структур в областях микроскопии высокого разрешения,
волноводной оптики, локального фотовозбуждения, нелинейной оптики. На основе
дальнейшего развития предложенной ранее технологии глубокого фотоанодного
травления (ГФАТ) кремния [11-13] изготовлена трехмерная
пространственно-периодическая структура ФК.
Методика и результаты вычислений
Для исследования распределения
поля в ФЗЗ-структурах использовался численный FDTD-метод решения уравнений
Максвелла [14,15]. При этом граничные условия должны быть сформулированы таким
образом, чтобы световая волна, достигшая границы, полностью поглощалась ею без
отражения обратно. К сожалению, для двух- и трехмерных задач не существует
идеально поглощающих и достаточно простых граничных условий. В наших расчетах
использовались поглощающие граничные условия второго рода. Эти условия
наилучшим образом позволяют снизить влияние отражения от границ на точность
численных расчетов [15].
В качестве объекта исследования
была выбрана структура, состоящая из переменного числа периодов (от пяти до
десяти) цилиндрических воздушных пор, образующих треугольную решетку в матрице
кремния. Для введения дефекта в двумерной ФЗЗ-структуре удалялся один из рядов
воздушных пор. Поскольку в области полной запрещенной зоны в выбранной нами
треугольной решетке воздушных цилиндров в кремнии глубина проникновения
светового поля в ФК (скин-слой) не превышает одного периода структуры, для определения
спектра пропускания решетки с дефектом рассматривались структуры, в которых
дефект вносился периодическим образом (с периодом 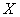 вдоль оси
вдоль оси 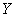 ). Другими словами, фактически решалась задача о распространении
света в сверхрешетке.
). Другими словами, фактически решалась задача о распространении
света в сверхрешетке.
Контрольные расчеты,
выполненные для сверхрешеток, различающихся только периодом 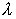 , показали, что распределение электромагнитного поля в
дефектной моде и спектр дефектных мод не зависят от периода
, показали, что распределение электромагнитного поля в
дефектной моде и спектр дефектных мод не зависят от периода 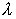 . Помимо удобства такая схема расчетов позволяет определить
уровень шумов, связанных с влиянием света, локализованного в соседних дефектах
(cross talk), что представляет
интерес для приложений подобных ФЗЗ-структур в системах оптической памяти и
оптической обработки информации. Вычисления продолжались до тех пор, пока не
переставали меняться усредненные по периоду значения электрического и
магнитного поля и их квадратов. Выходными данными являлись усредненные по
периоду квадраты (интенсивности) электрического и магнитного полей. На
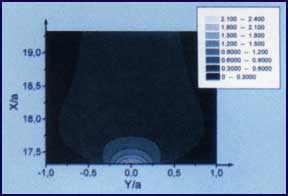
рис. 1 приведены двумерные распределения среднего квадрата электрического
поля
. Помимо удобства такая схема расчетов позволяет определить
уровень шумов, связанных с влиянием света, локализованного в соседних дефектах
(cross talk), что представляет
интерес для приложений подобных ФЗЗ-структур в системах оптической памяти и
оптической обработки информации. Вычисления продолжались до тех пор, пока не
переставали меняться усредненные по периоду значения электрического и
магнитного поля и их квадратов. Выходными данными являлись усредненные по
периоду квадраты (интенсивности) электрического и магнитного полей. На
рис. 1 приведены двумерные распределения среднего квадрата электрического
поля 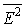 в ФЗЗ-структуре
описанного выше типа, состоящей из десяти периодов вдоль оси
в ФЗЗ-структуре
описанного выше типа, состоящей из десяти периодов вдоль оси 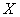 с периодом дефектов,
равным
с периодом дефектов,
равным 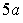 , для отношения
, для отношения 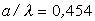 . Анализ пространственного распределения электромагнитного
поля показывает, что в данной структуре свет испытывает каналирование вдоль
дефекта, поле при этом локализовано в центре дефекта. На некоторых участках
канала диаметр пучка оказывается порядка
. Анализ пространственного распределения электромагнитного
поля показывает, что в данной структуре свет испытывает каналирование вдоль
дефекта, поле при этом локализовано в центре дефекта. На некоторых участках
канала диаметр пучка оказывается порядка 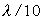 (см. рис. 1), что
в 5 раз меньше дифракционного предела для светового пучка, сфокусированного в
воздухе. Интенсивность света в центре дефекта в несколько сот раз выше
интенсивности на краях канала, что свидетельствует о высоком контрасте
каналирования пучка. Групповая скорость света при этом существенно уменьшается,
что указывает на возможность использования дефектных мод ФЗЗ-структур для
создания управляемых линий оптической задержки, аналогично оптическим линиям
задержки на основе одномерных ФЗЗ-структур, описанных в работе [16].
(см. рис. 1), что
в 5 раз меньше дифракционного предела для светового пучка, сфокусированного в
воздухе. Интенсивность света в центре дефекта в несколько сот раз выше
интенсивности на краях канала, что свидетельствует о высоком контрасте
каналирования пучка. Групповая скорость света при этом существенно уменьшается,
что указывает на возможность использования дефектных мод ФЗЗ-структур для
создания управляемых линий оптической задержки, аналогично оптическим линиям
задержки на основе одномерных ФЗЗ-структур, описанных в работе [16].
Распределение среднего квадрата
напряженности электрического поля 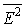 на выходе
ФЗЗ-структуры представлено на рис. 2. Поле в данных условиях локализовано
в поперечном направлении на пространственном масштабе, меньшем длины волны
излучения (
на выходе
ФЗЗ-структуры представлено на рис. 2. Поле в данных условиях локализовано
в поперечном направлении на пространственном масштабе, меньшем длины волны
излучения (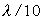 ), и спадает экспоненциально вдоль оси
), и спадает экспоненциально вдоль оси 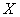 . Свойства данного поля подобны свойствам нерадиационной
волны, локализуемой вблизи поверхности образца в микроскопии ближнего поля, что
открывает возможность использования ФЗЗ-структур в качестве элементов
оптической микроскопии ближнего поля [17], осуществляющих эффективное
формирование нерадиационных волн. На основе принципа взаимности получаем, что
ФЗЗ-структуры с дефектом решетки могут быть также использованы для анализа
нерадиационного поля вблизи образца, что позволяет реализовать режим сбора
информации в микроскопии ближнего поля.
. Свойства данного поля подобны свойствам нерадиационной
волны, локализуемой вблизи поверхности образца в микроскопии ближнего поля, что
открывает возможность использования ФЗЗ-структур в качестве элементов
оптической микроскопии ближнего поля [17], осуществляющих эффективное
формирование нерадиационных волн. На основе принципа взаимности получаем, что
ФЗЗ-структуры с дефектом решетки могут быть также использованы для анализа
нерадиационного поля вблизи образца, что позволяет реализовать режим сбора
информации в микроскопии ближнего поля.
|

|
|
|
Рис. 1. Двухмерное распределение электрического поля в ФЗС-структуре
|
Рис. 2. Распределение среднего квадрата 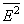 на выходе
ФЗЗ-структуры на выходе
ФЗЗ-структуры
|
|
|
|
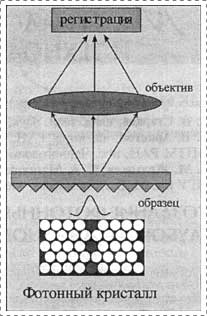
Рис.
3. Схема оптической микроскопии ближнего поля
|
Возможности достижения высокого
пространственного разрешения измерений, проводимых с помощью светового поля,
формируемого ФЗЗ-структурой рассматриваемого типа, были продемонстрированы расчетами
[17]. Результаты этих расчетов показывают, что неизлучающие волны, формируемые
в дефектных модах фотонных кристаллов, позволяют реализовать схемы оптической
микроскопии ближнего поля (рис. 3) с пространственным разрешением,
превышающим длину волны падающего излучения, и достаточно высоким отношением
сигнал/шум.
Несмотря на то, что вся энергия
излучения в нерадиационных волнах распространяется лишь вдоль выходной
поверхности ФЗЗ-структуры, не отрываясь от нее, высокая концентрация светового
поля на выходе подобной структуры может приводить к физически наблюдаемым
явлениям в ближней зоне. Это поле может быть использовано, в частности, для
локального возбуждения атомов либо молекул, если их разместить на месте
исследуемого образца (рис. 3).
Технология изготовления трехмерных
периодических структур на основе макропористого кремния
Технология изготовления
двумерных периодических структур из макропористого кремния на основе методики
глубокого фотоанодного травления n-Si
была достаточно подробно описана в работе [11]. Авторы работы [9] сформировали
систему макропористых областей кремния, разделенных с помощью фотолитографии и
глубокого травления в плазме SF6
топологическими дорожками. Авторы назвали полученную структуру трехмерной.
Однако, с точки зрения ФЗЗ, такая структура не может считаться трехмерной. В
работе [8] предложены различные варианты коллоидных кристаллов, представляющих
собой трехмерно-периодические структуры, полученные путем плотной упаковки тем
или иным способом сферических объектов с одинаковыми размерами. В качестве
таких сфер могут выступать плотноупакованные SiO2-сферы (см. работы
Yoshino К. с соавторами). В этом случае
f.c.с.-структуры (face-centered cubic structure) с воздушными прослойками между сферами
получили название синтетических опалов. К недостаткам синтетических опалов, так
же, как и других коллоидных кристаллов, следует отнести значительную
проблематичность контролируемого введения в структуру необходимых дефектов, что
является следствием метода самоорганизации в процессе создания таких структур (self-assembly method). Это
обстоятельство существенно ограничивает область применения коллоидных
кристаллов в качестве ФК-структур, поскольку, как это было показано в предыдущем
разделе, контролируемое присутствие дефектов в структуре лежит в основе
значительной области применения устройств на базе ФК.
Наиболее близким приближением к
трехмерной структуре ФК на основе макропористого кремния является структура,
предложенная в [12]. Как и в работах [9,11], периодичность оптических свойств
по осям 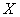 и
и 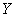 в предлагаемом
авторами варианте достигается периодичным расположением цилиндрических макропор
в матрице кремния. Контролируемое введение дефектов в указанную структуру
реализуется при нарушении периодичности расположения пор, что обеспечивается
соответствующим изменением топологии фотошаблона, задающего требуемую
периодичность затравочных
в предлагаемом
авторами варианте достигается периодичным расположением цилиндрических макропор
в матрице кремния. Контролируемое введение дефектов в указанную структуру
реализуется при нарушении периодичности расположения пор, что обеспечивается
соответствующим изменением топологии фотошаблона, задающего требуемую
периодичность затравочных 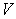 -образных канавок [12]. В третьем направлении (по оси
-образных канавок [12]. В третьем направлении (по оси 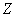 ) периодичность создается изменением диаметра пор.
) периодичность создается изменением диаметра пор.
Известно, что в зависимости от
условий термического окисления монокристаллического кремния (окисление –
влажное, сухое, в парах хлора и т.д.) объем окисленного материала возрастает в
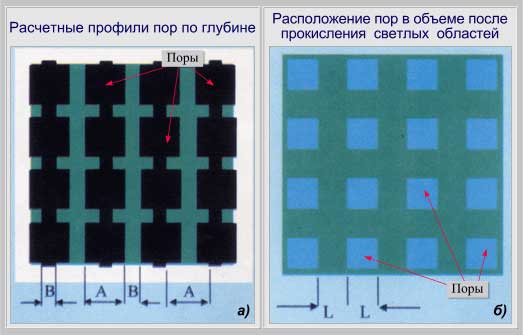
2-2,3 раза. Исходя из этого, несложно предложить структуру пор по глубине,
которая изображена на рис. 4,а в виде черных областей. В такой структуре
после полного прокисления матрицы кремния (зеленые области на рис. 4,а) может
быть реализована некая структура “обращенного опала” (рис. 4,б). В
рассматриваемом случае более тонкие части пор должны сомкнуться за счет
расширения кремния при его окислении, а более широкие части пор в результате
окажутся захлопнутыми и сформируют газовые области (светлые участки на
рис. 4,б), расположение которых строго определяется
конструктивно-технологическими параметрами процессов ГФАТ и окисления кремния.
Остальная часть структуры (зеленого цвета на рис. 4,б) представляет собой
окисленный кремний SiO2. В
идеализированном варианте (увеличение объема при окислении в 2 раза) размер 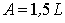 , а размер
, а размер 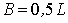 . Следует отметить, что на практике приходится учитывать
необходимость прокисления в первую очередь наиболее глубоких областей структуры,
затем последовательно – выше расположенных слоев, что объясняется
необходимостью доставки газообразного кислорода в область окисления. Поэтому геометрические
размеры будут несколько отличными от изображенных на рис. 4,а.
. Следует отметить, что на практике приходится учитывать
необходимость прокисления в первую очередь наиболее глубоких областей структуры,
затем последовательно – выше расположенных слоев, что объясняется
необходимостью доставки газообразного кислорода в область окисления. Поэтому геометрические
размеры будут несколько отличными от изображенных на рис. 4,а.
|
|
|
Рис. 4. Расчетная схема формирования структуры типа
“обращенного опала”
|
|
|
|
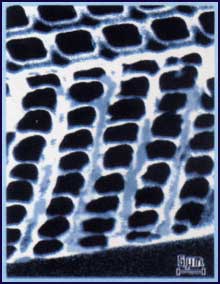
Рис. 5. РЭМ-изображение скола
кремниевой пластины с трехмерно-периодичекой структурой пор по глубине
|
Как было показано в работах [11,12],
при реализации в схеме ГФАТ режима генератора напряжения становится возможным
контроль за силой тока травления с помощью степени подсветки образца в процессе
травления. Это создает возможность целенаправленного изменения формы пор по
глубине. Представленный на рис. 5 фрагмент скола кремниевой структуры был
получен на кремнии  -типа проводимости с ориентацией поверхности (100) и удельным
сопротивлением 7-20 Ом×см
при ГФАТ в 3%-ном водном растворе плавиковой кислоты и периодической модуляцией
фототока травления с 10 до 1 мА×см-2.
При этом на поверхности кремниевой пластины предварительно формировались
обратные пирамиды травления с площадью основания 4´4 мкм2 [11]. На рис. 5
представлена периодическая структура без введенных дефектных плоскостей.
Дальнейшая оптимизация геометрических размеров элементов подобных структур с
учетом проведенных в настоящей работе расчетов позволит создать квазитрехмерные
ФК на основе как самого кремния, так и его оксида – структуры типа обращенного
опала. При этом конструктивно-технологические характеристики применяемых
процессов позволяют формировать структуры ФК с требуемыми распределением
дефектных уровней в их запрещенных зонах с помощью стандартных приемов кремниевой
технологии.
-типа проводимости с ориентацией поверхности (100) и удельным
сопротивлением 7-20 Ом×см
при ГФАТ в 3%-ном водном растворе плавиковой кислоты и периодической модуляцией
фототока травления с 10 до 1 мА×см-2.
При этом на поверхности кремниевой пластины предварительно формировались
обратные пирамиды травления с площадью основания 4´4 мкм2 [11]. На рис. 5
представлена периодическая структура без введенных дефектных плоскостей.
Дальнейшая оптимизация геометрических размеров элементов подобных структур с
учетом проведенных в настоящей работе расчетов позволит создать квазитрехмерные
ФК на основе как самого кремния, так и его оксида – структуры типа обращенного
опала. При этом конструктивно-технологические характеристики применяемых
процессов позволяют формировать структуры ФК с требуемыми распределением
дефектных уровней в их запрещенных зонах с помощью стандартных приемов кремниевой
технологии.
Выводы
Таким образом, разработанная
технология обработки кремния с использованием глубокого анодного травления с
периодической модуляцией тока травления во времени позволяет изготавливать
трехмерные периодические структуры на основе макропористого кремния. Подобная
методика дает возможность получать трехмерные периодические структуры с
размером пространственного периода порядка микрона и менее и представляется в
связи с этим чрезвычайно перспективной для изготовления трехмерных структур с фотонными
запрещенными зонами и контролируемым расположением дефектных уровней в
запрещенной зоне.
Выполненный анализ
распределения электромагнитного поля в двумерных ФЗЗ-структурах с дефектом
решетки и исследование спектра дефектных мод в запрещенных зонах таких структур
позволили выявить ряд важных свойств локализации поля в фотонных кристаллах.
Световое поле в этих условиях может быть локализовано в области размером менее
длины волны, а поле на выходе ФЗЗ-структуры обладает свойствами нерадиационной
волны, что позволяет достичь пространственного разрешения в ближнем поле, существенно
меньшем длины волны излучения.
Режимы распространения световых
пучков, которые могут быть реализованы с помощью ФЗЗ-структур, представляются
перспективными для решения целого ряда задач оптической микроскопии ближнего
поля, повышения плотности хранения информации в устройствах оптической памяти,
а также увеличения эффективности нелинейно-оптических взаимодействий.
Список литературы
1.
Yablonovitc Е. // J. Opt. Soc. Am. В. 1993. V. 10. P. 283-295;
Soukoulis C. Photonic Band Gap Materials // Ed., Dordrecht: Kluwer
Academic, 1996; Joannopoulos J., Meade R. and Winn J. //
Photonic Crystals, Princeton: Princeton Univ., 1995.
2.
Baba T.
and Matsuzaki T. // Jpn. J. Appl. Phys., 1996. Part 1, 35, № 2B. P.
1348.
3.
Cheng C.C.
and Scherer A. // J. Vacuum Sci. Technol. B, 1995, 13, № 6. P. 2696.
4.
Berger V.,
Gauthier-Lafaye O. and Costard // E., Electron. Lett. 1997, 33, № 5.
P. 425.
5.
Borisov R.A.,
Dorojkina G.N., Koroteev N.I., Kozenkov V.M.,
Magnitskii S.A., Malakhov D.V., Tarasishin A.V.,
Zheltikov A.M. // Appl. Phys. B, 67, 1998, 765.
6.
Knight J.C.,
Birks T.A., Russel P. St. J. and Atkin D.M. // Opt.
Lett., 1996, 21, 1547.
7.
Tarhan I.I.
and Watson G.H. Photonic Band Gaps and Localization / Ed. С. М. Soukoulis New York: Plenum. 1993. P. 93.
8.
Astratov V.N.,
Vlasov Yu.A., Karimov O.Z., Kaplyanskii A.A.,
Musikhin Yu.G., Bert N.A., Bogomolov V.N. and
Prokofiev A.V. // Phys. Lett. A. 1996. Vol. 222, P. 349-353;
Bogomolov V.N., Gaponenko S.V., Kapitonov A.M., Prokofiev A.V.,
Ponyavina A.N., Silvanovich N.I. and Samoilovich S.M. // Appl.
Phys. A. 1996. Vol. 63. P. 613; Vlasov Yu.A., Astratov V.N.,
Karimov O.Z., Kaplyanskii A.A., Bogomolov V.N. and Prokofiev A.V.
// Phys. Rev. B. 1997. Vol. 55. P. 13357; Yoshino K., Tada K.,
Ozaki M., Zakhidov A.A. and Baughman R.H. // Jpn. J. Appl. Phys.
1997. Part 2, 36. № 6A. P. L714; Yoshino K., Saton S.,
Shimoda Yu., Kawagishi Yo., Nakayama K. and Ozaki M. //
Jpn. J. Appl. Phys. 1999. Vol. 38. P. L961-L963.
9.
Ottow S.,
Lehmann V., Foll H. // J. Electrochem. Soc., 1996. 143. P. 385.
10. Fleming J.G., Lin S.-Y. //
Opt. Lett. 1999. Vol. 24. P. 49.
11. Aristov V.V.,
Starkov V.V., Schabel'nikov L.G., Kuznetsov S.M.,
Ushakova A.P., Grigoriev M.V., Tseitlin V.M. // Optics
Communication. 1999. Vol. 161. P. 203-208.
12. Aristov V.V.,
Magnitsii S.A., Starkov V.V., Tarasishin A.V. and
Zheltikov A.M. // Laser Physics. 1999. Vol. 9, № 6. P. 1-6.
13. Gruning U., Lehmann V.,
Ottow S., Busch K. // Appl. Phys. Lett. 1996. Vol. 68. P. 747-749.
14. Taflove A. Computational
Electrodynamics: The Finite-Difference Time-Domain Method // Norwood, MA:
Artech House. 1995.
15. Желтиков А.М.,
Магницкий С.А., Тарасишин А.В. // ЖЭТФ. 2000. Vol. 117. Вып. 4. С. 1-10.
16. Scalora M., Flynn R.J.,
Reinhardt S.В.,
Fork R.L., Bloemer M.J., Tocci M.D., Bowden C.M.,
Ledbetter H., Bendickson J., Dowling J.P., Leavitt R.P. //
Phys. Rev. 1996. Vol. 54, P. R1078.
17. Желтиков А.М.,
Магницкий С.А., Тарасишин А.В. // Письма ЖЭТФ. 1999. Vol. 70, P. 323; Magnitskii S.A., Tarasishin A.V.,
Zheltikov A.M. // Appl. Phys. B. December 1999, Vol. 69.
![]()
![]() -типа проводимости с ориентацией поверхности (100) и удельным
сопротивлением 7-20 Ом×см
при ГФАТ в 3%-ном водном растворе плавиковой кислоты и периодической модуляцией
фототока травления с 10 до 1 мА×см-2.
При этом на поверхности кремниевой пластины предварительно формировались
обратные пирамиды травления с площадью основания 4´4 мкм2 [11]. На рис. 5
представлена периодическая структура без введенных дефектных плоскостей.
Дальнейшая оптимизация геометрических размеров элементов подобных структур с
учетом проведенных в настоящей работе расчетов позволит создать квазитрехмерные
ФК на основе как самого кремния, так и его оксида – структуры типа обращенного
опала. При этом конструктивно-технологические характеристики применяемых
процессов позволяют формировать структуры ФК с требуемыми распределением
дефектных уровней в их запрещенных зонах с помощью стандартных приемов кремниевой
технологии.
-типа проводимости с ориентацией поверхности (100) и удельным
сопротивлением 7-20 Ом×см
при ГФАТ в 3%-ном водном растворе плавиковой кислоты и периодической модуляцией
фототока травления с 10 до 1 мА×см-2.
При этом на поверхности кремниевой пластины предварительно формировались
обратные пирамиды травления с площадью основания 4´4 мкм2 [11]. На рис. 5
представлена периодическая структура без введенных дефектных плоскостей.
Дальнейшая оптимизация геометрических размеров элементов подобных структур с
учетом проведенных в настоящей работе расчетов позволит создать квазитрехмерные
ФК на основе как самого кремния, так и его оксида – структуры типа обращенного
опала. При этом конструктивно-технологические характеристики применяемых
процессов позволяют формировать структуры ФК с требуемыми распределением
дефектных уровней в их запрещенных зонах с помощью стандартных приемов кремниевой
технологии.



